Abstract
Multi-robot co-manipulation shows great potential to address the limitations of using single robot in complicated tasks such as robotic surgeries. However, the dynamic setup poses great uncertainties in the circumstances of robotic mobility and unstructured environment. Therefore, the relationships among all the base frames (robot-robot calibration) and the relationships between the end-effectors and the other devices such as cameras (hand-eye calibration) and tools (tool-flange calibration) have to be determined constantly in order to enable robotic cooperation in the constantly changing environment. We formulated the problem of hand-eye, tool-flange and robot-robot calibration to a matrix equation AXB=YCZ. A series of generic geometric properties and lemmas were presented, leading to the derivation of the final simultaneous algorithm. In addition to the accurate iterative solution, a closed-form solution was also introduced based on quaternions to give an initial value. To show the feasibility and superiority of the simultaneous method, two non-simultaneous methods were also proposed for comparison. Furthermore, thorough simulations under different noise levels and various robot movements were carried out for both simultaneous and non-simultaneous methods. Experiments on real robots were also performed to evaluate the proposed simultaneous method. The comparison results from both simulations and experiments demonstrated the superior accuracy and efficiency of the simultaneous method.
Problem Formulation
Measurement Data:
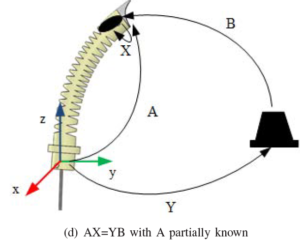
Homogeneous transformations from the robot bases to end-effector (A and C), and from tracker to marker (B).
Unknowns:
Homogeneous transformations from one robot base frame to another (Y), and from eye/tool to robot hand/flange (X and Z).
The measurable data A, B and C, and the unknowns X, Y and Z form a transformation loop which can be formulated as, AXB=YCZ (1).

Fig. 1: The relevance and differences among the problem defined in this paper and the other two classical problems in robotics. Our problem formulation can be considered as a superset of the other two.
Approaches
Non-simultaneous Methods
3-Step Method
In the non-simultaneous 3-Step method, the X and Z in (1) are separately calculated as two hand-eye/tool-flange calibrations which can be represented as an AX = XB problem in the first and second steps. This results in two data acquisition procedures, in which the two manipulators carry out at least two rotations whose rotational axes are not parallel or anti-parallel by turns while the other one being kept immobile. The last unknown robot-robot relationship Y could be solved directly using the previously retrieved data by the method of least squares.
2-Step Method
The non-simultaneous 2-Step method formulates the original calibration problem in successive processes which solve AX = XB firstly, and then the AX = YB. The data acquisition procedures and obtained data are the same with the 3-Step method. In contrast to solving robot-robot relationship independently, the 2-Step method solves tool-flange/hand-eye and robot-robot transforms in an AX = YB manner in the second step. This is possible because equation AXB = YCZ can be expressed as (AXB)inv(Z) = YC, which is in an AX = YB form with the solution of X known.
Simultaneous Method
Non-simultaneous methods face a problem of error accumulation, since in these methods the latter steps use the previous solutions as input. As a result, the inaccuracy produced in the former steps will accumulate to the subsequent steps. In addition to accuracy, it is preferred that the two robots participating the calibration procedure simultaneously, which will significantly save the total time required.
In regards to this, a simultaneous method is proposed to improve the accuracy and efficiency of the calibration by solving the original AXB = YCZ problem directly. During the data acquisition procedure, the manipulators simultaneously move to different configurations and the corresponding data set A, B and C are recorded. Then the unknown X, Y and Z are solved simultaneously.
Evaluations
Simulations
To illustrate the feasibility of the proposed methods, intensive simulations have been carried out under different noise situations and by using different numbers of data sets.

Fig. 2: A schematic diagram which shows the experiment setup consisting of two Puma 560 manipulators, a tracking sensor and a target marker to solve the hand-eye, tool-flange and robot-robot calibration problem.
Simulations Results
For the rotational part, the three methods perform evenly in the accuracy of Z. However, the simultaneous method slightly outperforms in the accuracy of X and significantly in the accuracy of Y than the other two non-simultaneous methods. The results of the translational part are similar to the rotational ones. For the solution of Z, the accuracy of the simultaneous method is as good as the 3-Step method but slightly worse than the 2-Step method. However, the simultaneous method achieves a significantly improvement in the accuracy of X and Y compared to the other two methods.



Experiments Results
Besides the simulation, ample real experiments have been conceived and carried out under different configurations to evaluate the proposed methods. As shown in Fig. 6, the experiments involved a Staubli TX60 robot (6 DOFs, averaged repeatability 0.02mm), a Barrett WAM robot (4 DOFs, averaged repeatability 0.05mm) and a NDI Polaris optical tracker (RMS repeatability 0.10mm). The optical tracker was mounted to the last link of the Staubli robot, referred to as sensor robot. The corresponding reflective marker was mounted to the last link of the WAM robot, referred to as marker robot.

Fig. 6: The experiment is carried out by using a Staubli TX60 robot and a Barrett WAM robot. A NDI Polaris optical tracker is mounted to the Staubli robot to track a reflective marker (invisible from current camera angle) that is mounted to the WAM robot.
To demonstrate the superiority of the simultaneous method in the real experimental scenarios, a 5-fold cross-validation approach is implemented for 200 times for all the calibration methods under all system configurations. For simultaneous method, after data alignment and RANSAC processing, 80% of the remaining data are randomly selected to calculate unknown X, Y, and Z, and 20% are used as test data to evaluate the performance. For 2-Step and 3Step methods, after calculating the unknowns by each method, same test data from the simultaneous method are used to evaluate their performances.
In Fig. 7, the evaluated errors of 200 times 5-fold cross-validation for three proposed methods at three ranges are shown as box plots. Left-tail paired-samples t-tests have been carried out to compare the performances of simultaneous method versus 2-Step and 3-Step methods, respectively. The results indicate that the rotational and translational errors from the simultaneous method are very significantly smaller than the 2-Step and 3-Step methods. Only two non-significant results exist in the rotational performances at medium and far ranges when comparing the simultaneous method with the 3-Step one. Nevertheless, the simultaneous method outperforms the non-simultaneous ones for translation error at all ranges.

Fig. 7: Results of 200 times 5-fold cross-validation and left-tail paired-samples t-test at the near, medium and far ranges. The box plots show the rotational and translational error distributions for three methods at three ranges. **, * and N.S. stands for very significant at 99% confidence level, significant and non-significant at 95% confidence level.
Related Publications
1. Liao Wu, Jiaole Wang, Max Q.-H. Meng, and Hongliang Ren, imultaneous Hand-Eye, Tool-Flange and Robot-Robot Calibration for Multi-robot Co-manipulation by Solving AXB = YCZ Problem, Robotics, IEEE Transactions on (Conditionally accepted)
2. Jiaole Wang, Liao Wu and Hongliang Ren, Towards simultaneous coordinate calibrations for cooperative multiple robots, Intelligent Robots and Systems (IROS 2014), 2014 IEEE/RSJ International Conference on. IEEE, 2014: 410-415.
Institute & People Involved
The Chinese University of Hong Kong (CUHK): Jiaole Wang, Student Member, IEEE; Max Q.-H. Meng, Fellow, IEEE
National University of Singapore (NUS): Liao Wu; Hongliang Ren, Member, IEEE
Videos
-Calibration Experiments